- お金の価値は相対的で、時間とともに変動する。お金を交換可能な「品物」と捉えることが、お金を数学的に考える第一歩である。
- お金を効率的に増やすには、指数関数的に成長する「種」を見つけることである。
- 組み合わせの数学を利用して過去のデータを検証すれば、ギャンブルの勝率を細かい部分まで予測することができる。
- 今の世界を支配しているのは数学的なアルゴリズムだが、未来の世界を支配するのもまた、数学を駆使した者だろう。
数学的思考で資産を増やす方法

お金の本質を理解する:相対的価値と主観性
お金は単なる紙切れや金属片ではない。それは価値を計測し、比較するための「数学的ツール」なのだ。
古代社会では物々交換が主流だった。農民が収穫した穀物を、職人の作った鍋や道具と直接交換していた。しかし、この仕組みには根本的な問題がある。交換したい双方が、互いに相手の持つものを欲していなければ取引は成立しない。
社会が複雑化すると、多者間の取引調整が困難になる。この課題を解決するために金融システムが誕生した。お金は取引の仲介役となり、その価値は他の商品やサービスとの相対的な関係で決まる。
重要なのは、お金の価値が時間とともに絶えず変動し、状況に応じて主観的に決まることだ。清流のほとりに住む人にとって水は無価値でも、砂漠で渇きに苦しむ人には何百万円の価値を持つ。
資産管理の核心は、この価値の変動と差異を見極めることにある。純資産(全資産から負債を差し引いた金額)の概念で考えると理解しやすい。お金を「交換可能な品物」として捉えることが、数学的な資産管理の出発点となる。
複利の威力を測る「72の法則」

投資元本が2倍になるまでの期間を素早く計算する方法がある。それが15世紀の数学者ルカ・パチョーリが『スムマ』で紹介した「72の法則」だ。
計算方法は驚くほどシンプル。72を年利率で割るだけで、元本が倍増するまでの年数がわかる。年利6%なら72÷6=12年、年利9%なら72÷9=8年という具合だ。
この法則は概算であり、年利5〜10%の範囲で最も正確だ。しかし、何世紀にもわたって投資家に愛用されてきた実績が、その実用性を物語っている。
指数関数的成長の「魔法」
1000ポンドを1年で100万ポンドにする方法を考えてみよう。
仮に「必ず2倍の値段で売れる魔法の豆」があったとする。1000ポンドで購入し、2000ポンドで売却。翌週、2000ポンドで2倍の量を購入し、4000ポンドで売却。これを10週間続けると、102万4000ポンドになる。
現実に魔法の豆は存在しない。しかし、この例が示すのは指数関数的成長の威力だ。継続的に利益を生み出すプロセスを見つけ、それを反復することが資産形成の鍵となる。
実際の投資市場を見ると、不動産や株式は長期的に安定した成長を示している。1984年にイギリスで10万ポンドを投資した場合、2015年には不動産で50万2500ポンド(年利5.7%)、株式で53万3000ポンド(年利5.9%)に成長していた。配当再投資を含めた株式投資なら、153万3500ポンドという驚異的な結果だ。
真の富の源泉
労働で給料を2倍、10倍にすることは可能かもしれない。しかし、100倍以上の富を築くには、どこかで指数関数的成長の「種」を見つけることが不可欠だ。
世界の富豪たちが巨万の富を築いた理由の一つがここにある。彼らは単に働くのではなく、数学的な成長パターンを理解し、それを活用したのだ。
資産形成の本質は、お金の相対的価値を理解し、時間の経過とともに複利効果を最大化することにある。数学的思考は、この目標を達成するための強力な武器なのである。
KISSポートフォリオ9つの基本ルール ①お金は若いうちから定期的に貯めよう 若いうちから貯金の習慣をつけると、将来的に経済的な安心感が得られますし、投資や資産運用のチャンスも広がります。特に「先取り貯金」や「自動積立」などを[…]
統計学的思考で損失を回避する方法
確率論の誕生:数学者たちのギャンブル解析
16世紀のイタリアの数学者ジェロラモ・カルダーノは、確率論の父として知られる。彼は著書『サイコロ遊びについて』で、ギャンブルを数学的に分析する手法を確立した。
カルダーノの手法は明快だった。まず起こりうる結果をすべて列挙し、その中で有利な結果が占める割合を計算する。2個のサイコロで6のゾロ目が出る確率を考えてみよう。全ての組み合わせは36通り、ゾロ目は6通り、6のゾロ目は1通りのみ。したがって確率は36分の1(約2.8%)となる。
1世紀後、哲学者ブレーズ・パスカルと数学者ピエール・ド・フェルマーは「賭け金の分配問題」に取り組んだ。7点先取のゲームが6対4で中断した場合、賭け金をどう分配すべきか。彼らは「期待値」の概念を導入し、ゲームの全ての可能な結末を考慮して公正な分配を計算した。
この思考プロセスこそ現代確率論の核心であり、「パスカルの三角形」として知られる組み合わせ計算法の基礎となった。現代のギャンブル理論やスポーツ賭博の予測システムも、この組み合わせ数学を応用している。
変動性を理解する:金持ちと貧乏人のコイン投げ

ギャンブルには必ずボラティリティ(変動性)が存在する。この変動性を測る統計学の指標が「標準偏差」だ。標準偏差は、データが平均値からどれだけ散らばっているかを示す。
「68-95-99.7則」という重要な法則がある。正規分布において、データの68%が平均から標準偏差1個分以内、95%が2個分以内、99.7%が3個分以内に収まることを示している。
具体例で考えてみよう。30ポンドを持つ金持ちと10ポンドを持つ貧乏人が、コイン投げで1ポンドずつ賭けるゲームを100回行う。負けが続いて手持ちが0ポンドを切ったら退場というルールだ。
100回のコイン投げの標準偏差は10ポンドとなる。68%の確率で結果はマイナス10ポンドから10ポンドの範囲に収まる。しかし、32%の確率で10ポンドを超える損失が発生する。
貧乏人は16%の確率で10ポンド以上の損失を被り、破産リスクが高い。一方、金持ちの元手30ポンドは標準偏差3個分に相当し、破産確率は極めて低い。ゲーム自体は公平でも、資金量の差が勝敗を大きく左右するのだ。
カジノが必ず勝つ理由:大数の法則

人間は統計を直感的に理解するのが苦手だ。数学を使って市場やゲームを予測する際は、不十分なデータや感情的な判断を避けることが重要だ。
「大数の法則」は、試行回数が増えるほど結果が理論値に近づく原理だ。カジノが確実に利益を上げるのは、この法則を活用しているからだ。
1台のルーレット盤を1時間だけ回すなら、カジノは大損する可能性がある。しかし50台を1か月間連続で回せば、ハウス・エッジ(カジノ側の利益率)の予測値に極めて近い結果となる。
小数の法則の落とし穴
一方、「小数の法則」は危険な錯覚を生む。少ない標本から性急に結論を導く傾向だ。
新人営業担当が3か月連続で売り上げを伸ばしたとする。つい優秀だと判断したくなるが、これは典型的な小数の法則の罠だ。ビギナーズ・ラックや前任者の顧客からのリピート注文の可能性も十分にある。
認知バイアスを避ける方法
人間は「利用可能性バイアス」に陥りやすい。記憶に残る直近の事例に基づいて確率を判断してしまう傾向だ。詐欺師はこのバイアスを悪用し、成功事例のみを強調して投資家を欺く。
バイアスから解放されるには、「時間」の価値を常に意識することだ。ビジネスや投資の判断では、潜在的なコスト削減や利益を測る基準として「時給」を活用する。
統計学的思考の実践
合理的な判断を下すためには、人間の本能的なバイアスを認識し、それを回避する努力が欠かせない。統計学的思考は、感情に流されず、データに基づいた冷静な判断を可能にする。
損失を回避し、長期的な成功を収めるためには、確率の正しい理解と、標準偏差やボラティリティの概念を実践的に活用することが重要だ。カジノが確実に勝つように、統計学的優位性を味方につけることで、不確実性の高い世界でも着実に成果を上げることができるのである。
個別株式投資とポーカーには多くの共通点がある。どちらもスキルと運の両方が必要で、リスク管理がものをいう。運がめぐってきたときにそれを活かせるかは、スキル次第だ。 エミン氏は、市場成長の可能性や個別の企業のシェアを見極め、銘柄を選ぶ[…]
数学で収益システムを構築する方法

Googleの成功を支える基礎数学
1995年、スタンフォード大学の大学院生だったセルゲイ・ブリンとラリー・ペイジは、インターネット検索の概念を根本から変革した。彼らが開発した「ページランク」アルゴリズムは、現在でもGoogleの検索エンジンの核心を成している。
当時の検索エンジンは単純だった。検索キーワードがページに何回出現するかを数え、その頻度でランキングを決めていた。しかし、ブリンとペイジは全く異なるアプローチを取った。「そのページにリンクしている他のページの数と質」を評価指標に加えたのだ。
驚くべきは、この革命的なアイデアが大学1年生レベルの数学に基づいていることだ。彼らが使ったのは「行列の固有ベクトルと固有値」という、線形代数の基本概念だった。
ページランクの数学的仕組み
アルゴリズムの動作原理は反復計算にある。まず各ページに適当な確率値を割り当て、その後で特定の関数を繰り返し適用する。計算を重ねるごとに結果が実際の値に収束していく。
一度正確な値に近づくと、その関数は毎回同じような結果を返すようになる。これにより、新しいページのみ初期推測値から開始し、既存のページは前回の計算結果を基に効率的に調整される。
この仕組みによって、Googleは250億以上のウェブページから最適な検索結果を瞬時に提供できるようになった。世界を変えた検索エンジンの核心が、実は大学初年度の数学にあったのだ。
Facebookのアルゴリズム経済学
アルゴリズムとは、問題解決や計算のための規則と演算の集合だ。Facebookは、このアルゴリズムを使って巨大な収益システムを構築している。
Facebookの仕組みは、ユーザーの行動データを絶えず収集・分析することで成り立っている。クリック、いいね、動画再生時間、広告の拒否、フォローしたグループ―あらゆる行動がアルゴリズムに入力される。
この膨大なデータは「関連性」の高い順序に並び替えられ、各ユーザーに最適化されたコンテンツが配信される。最近「いいね」した人の投稿を多めに表示し、関心の薄いコンテンツを除外するといった調整が自動的に行われる。
フィルター・バブルの経済効果
こうしたアルゴリズムには意図しない副作用がある。ユーザーが好む情報のみを提供し続けることで、「フィルター・バブル」と呼ばれる情報の偏りが生じる。
しかし、これは企業にとって収益機会でもある。ユーザーの行動を予測しやすくなり、より効果的な広告配信が可能になる。アルゴリズムがユーザーの嗜好を学習すればするほど、広告の精度が向上し、収益が増加する構造だ。
アルゴリズムの影響力を理解する
もし「フィルター・バブル」から抜け出したいなら、意図的に普段見ないニュースソースをクリックしてみるとよい。アルゴリズムの仕組みを理解することで、その影響をある程度コントロールできる。
現代では、アルゴリズムと計量分析を駆使する「クオンツ」が世界中のビジネスを支配している。金融市場、電子商取引、ソーシャルメディア、動画配信―あらゆる分野でアルゴリズムが収益の源泉となっている。
次世代の数学的ビジネスモデル
今後数十年を支配する技術がなんであるかは、まだ明らかではない。しかし、確実に言えるのは、未来の勝者もまた数学を駆使して収益システムを構築するということだ。
人工知能、機械学習、ブロックチェーン、量子コンピューティング―これらの先端技術もすべて数学的な原理に基づいている。数学的思考を身につけることは、次世代の収益機会を見つけるための必須スキルなのである。
実践的な教訓
GoogleやFacebookの成功は、複雑に見える問題も基礎的な数学で解決できることを示している。重要なのは、数学の知識そのものよりも、問題を数学的に捉え、システム化して解決する思考法だ。
収益システムを設計する際は、以下の点を考慮すべきだ。
データの収集と分析:ユーザーの行動パターンを数値化し、継続的に分析する仕組みを構築する。
反復改善:アルゴリズムを継続的に調整し、精度を向上させる仕組みを組み込む。
スケーラビリティ:規模が拡大しても効率的に動作する数学的モデルを設計する。
予測可能性:過去のデータから未来の傾向を予測し、それを収益に結びつける。
数学は単なる学問ではなく、現代ビジネスの実践的な武器なのである。
資本収益率(r)が経済成長率(g)よりも大きければ、富の集中が生じ、格差が拡大する。歴史的に見るとほぼ常にrはgより大きく、格差を縮小させる自然のメカニズムなどは存在しない。 20世紀に格差が縮小した原因は1914―1945年の世[…]
数学的思考で経済的成功を掴む方法 – 投資とリスク管理の数学的戦略
ポートフォリオ理論による賢明な資産配分
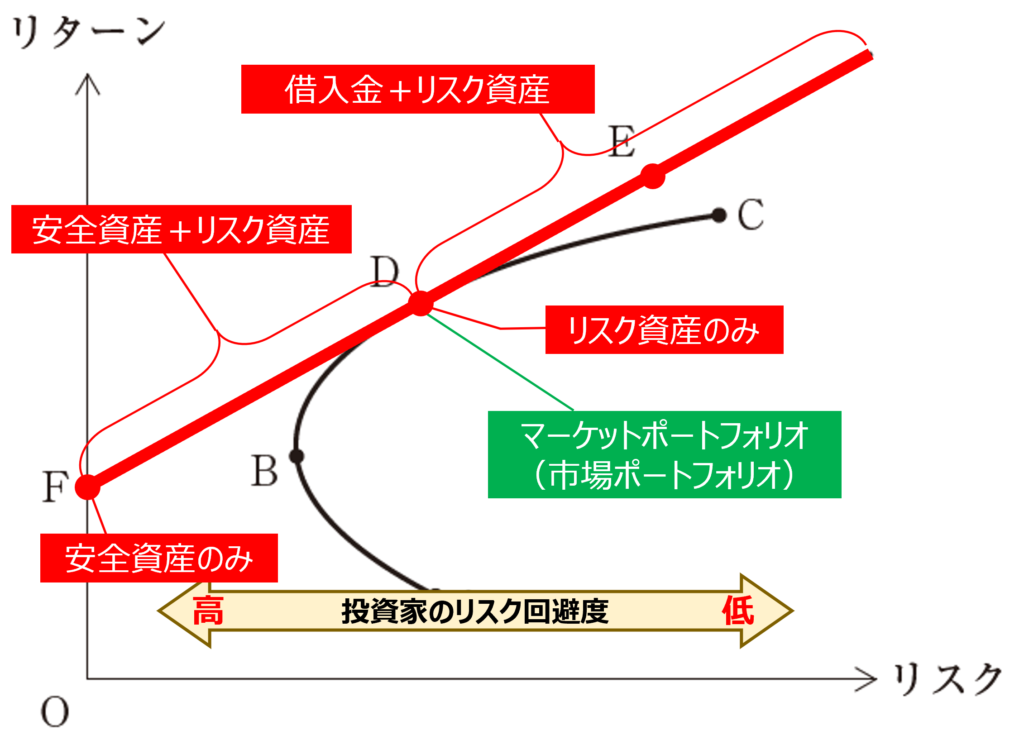
現代投資理論の基盤となる「ポートフォリオ理論」は、リスクを数学的に分析し、最適な資産配分を導き出す手法だ。単一の投資先に集中するのではなく、異なる特性を持つ資産に分散投資することで、全体のリスクを効率的に抑制できる。
この理論の核心は、各資産の相関関係を数値化し、リスクとリターンの最適なバランスを見つけることにある。数学的計算により、同じリスクレベルでより高いリターンを期待できる、または同じリターンでより低いリスクを実現できる投資組み合わせを特定する。
高速取引を支配するクォンツの世界
金融市場では「クォンツ」と呼ばれる数学的専門家たちが、高速取引システムを駆使して巨額の利益を上げている。彼らは複雑な数学的モデルを構築し、市場の微細な価格変動を瞬時に捉えて取引を実行する。
ミリ秒単位での取引判断、統計的裁定取引、機械学習アルゴリズムの活用―これらすべてが高度な数学的知識に基づいている。個人投資家には真似できない領域だが、その原理を理解することで市場の動向をより深く把握できる。
ウォーレン・バフェットも活用した「ケリー基準」
投資の神様と呼ばれるウォーレン・バフェットも活用してきた「ケリー基準」は、勝率と配当率から最適な投資比率を計算する数学的手法だ。
この基準は、長期的な資産成長を最大化するために、各投資機会にどの程度の資金を配分すべきかを数式で示す。感情に左右されがちな投資判断を、客観的な数学的根拠に基づいて行えるようになる。
人間心理と数学的思考の対立 – ギャンブラーの誤謬という心理的な罠
「ギャンブラーの誤謬」は、過去の結果が未来の確率に影響を与えるという錯覚だ。コインを5回連続で表が出た後、「次は裏が出やすい」と考えてしまう心理現象である。
しかし、数学的には各回の結果は独立しており、過去の結果は将来の確率に一切影響しない。この誤謬により、多くの人がギャンブルで損失を重ね、やめられなくなる。数学的思考を身につけることで、このような心理的な罠を避けることができる。
保険という合理的な「損」の選択
数学的に計算すれば、保険は期待値的には損をする取引だ。保険会社は数学的優位性を持って商品を設計し、確実に利益を上げる仕組みを構築している。
それでも多くの人が保険に加入するのは、「損失回避」という人間の心理的特性による。小さな確実な損失(保険料)を払って、大きな潜在的損失(事故や病気)を回避したいという心理が働く。これは数学的には非合理でも、人間にとっては合理的な選択といえる。
数学的知識の実践的価値 – 経済的成功の必須基盤
著者が強調するように、数学をしっかり理解することは経済的成功に欠かせない土台である。現代経済では、データ分析、確率計算、統計的思考が至る所で活用されている。
数学的思考を身につけることで、以下のような利点が得られる。
感情的な判断の回避:客観的なデータに基づいた意思決定が可能になる
リスクの適切な評価:潜在的な損失と利益を数値化して比較できる
長期的な視点の獲得:短期的な変動に惑わされず、長期トレンドを把握できる
投資機会の発見:他の人が見落とす数学的優位性を見つけられる
今からでも遅くない数学力の向上 – 実践的な学習アプローチ
数学力を鍛えることは、年齢に関係なく可能だ。重要なのは、抽象的な数学理論ではなく、実際の経済活動に応用できる数学的思考を身につけることである。
統計学の基礎:平均、標準偏差、相関係数などの基本概念を理解する
確率論の活用:期待値、リスク評価、意思決定への応用を学ぶ
複利計算:時間の価値と複利効果を数値的に把握する
データ分析:表計算ソフトを使った基本的な分析技術を習得する
継続的な実践の重要性
数学的思考は一朝一夕で身につくものではない。しかし、日々の投資判断や経済活動において意識的に数学的アプローチを取り入れることで、徐々に思考パターンが変化していく。
本書を出発点として、数学的知識を実際の経済活動に応用し、経済的成功のための確固たる土台を築いていくことが重要である。数学は単なる学問ではなく、現代社会を生き抜くための実践的な武器なのだ。
「不労所得」という言葉を耳にしたことがあるでしょうか?これは、働かなくても自動的にお金が入ってくる仕組みのことです。例えば、株式投資や不動産投資を通じて得られる配当金や家賃収入が代表的な例です。多くの人が経済的自由を求めて不労所得[…]












